Laboratorio #1 Conceptos Eléctricos

Laboratorio #1 Conceptos eléctricos

Andrés Julian Yepes Díaz

Conrrado Alberto

Institución Universitaria Salazar Y Herrera

2019

Introducción

En el laboratorio se realizó el montaje de un circuito eléctrico de resistencias en serie y leds en la Protoboard, con el objeto de hallar las medidas de su tensión, corriente y sus resistencias.

Materiales

Los materiales usados en el laboratorio fueron :

• Protoboard
• Multimetro
• Leds de color
• Resistencias
• Fuente de poder
• Caimanes

Procedimiento

Se realizó en primer lugar el montaje del circuito de la siguiente manera :

• Se pusieron tres resistencias en serie, sus equivalencias eran 330Ω, 470Ω y 1k  
• Al verificar que el circuito esta montado correctamente, se conectó la fuente
• Luego se hizo una interrupción en el circuito para tomar las medidas con el multimetro

Después  de hallar todas las medidas se realizó el montaje de un segundo circuito.

Y al realizar el montaje se llevaron a cabo nuevamente los pasos 1 y 2 del circuito anterior.


Cálculos del primer circuito

OBSERVACIONES 

• SE PUDO OBSERVAR EN EL LABORATORIO QUE ENTRE MAS RESISTENCIAS LA CORRIENTE SE MERMABA Y SE PUEDE UTILIZAR UN ARTEFACTO CON MENOS VOLTAJE SIN DAÑARLO.
• DEPENDIENDO EL VOLTAJE CAMBIA LA CORRIENTE QUE CIRCULA POR LA RESISTENCIA.
• OBVIAMENTE PARA MEDIR EL VOLTAJE SE UTILIZA UN MULTIMETRO PARA MEDIR CORRIENTE UN AMPERIMETRO Y PARA LA RESISTENCIA UN OHMETRO

CONCLUSIONES 

1. LO QUE NOS DEJA EL LABORATORIO ES QUE MIENTRAS ESTEMOS UTILIZANDO UNA PROTOBOARD, PODREMOS REALIZAR MONTAJES A UNA ESCALA MENOR PERO DESPUÉS PUEDEN SER A GRAN ESCALA O TRIDIMENSIONAL.
2. PARA TOMAR UNA CORRIENTE LO QUE SE DEBE HACER ES UNA INTERRUPCIÓN EN EL CIRCUITO Y PARA O DESCONECTAR EL VOLTAJE.
3. SI UNA CORRIENTE COMO EN EL CASO DE NUESTRO GRUPO NO NOS DA AMPERIOS O LA MEDICIÓN CORRECTA FUE PORQUE COMETIMOS UN ERROR Y PUDIMOS DAÑAR LA HERRAMIENTA UTILIZADA EN ESTE CASO EL AMPERIMETRO.

Ejercicio para el Cálculo de la Resistencia Equivalente

Ejercicio para el Cálculo de la Resistencia Equivalente
Según la Ley de ohm:

V = I • R

I = V/R

R = V/I

Tenemos un circuito compuesto por 6 resistencias puestas en modo mixto y queremos calcular la resistencia total del circuito (Figura.1). La fuente entrega un voltaje de 12 V.

Figura 1

Lo primero es agrupar resistencias que estén en el mismo modo de conexión. Así vemos que R2, R3 y R4 están en serie. Por lo tanto, podemos calcular su valor equivalente y sustituir:

4Ώ + 6Ώ + 8Ώ = 18Ώ

Entonces, podemos quitar las tres resistencias, y poner otra con el valor equivalente (Figura 2)

Figura 2

Ahora nos encontramos con dos resistencias en paralelo (R5 y Ra) de las que calcularemos su valor equivalente (Figura 3). Para ello calcularemos el inverso de la suma de los inversos de los ohmios de cada resistencia. Para hacer el inverso de un número se divide a uno por éste. Con esto, nos queda que 5Ω y 18Ω en paralelo es equivalente a 1/(1/5 + 1/18) = 3,913Ω

Figura 3

Ahora podemos eliminar R5 y Ra y poner en su lugar Rb que valdrá 3,913Ώ
Con esto, ya podemos hacer el cálculo final sumando las tres resistencias en serie que nos han quedado:

3Ώ + 3,9Ώ + 7Ώ,= 13,9.

Ya hemos hallado la resistencia total del circuito (13,9 ohmios) y ahora nos faltaba terminar de hallar el resto de valores de todo el circuito.

Para hallar la IT (intensidad total) debemos aplicar la ley de Ohm:

I = V/R

con lo que tenemos que IT = 12/13,9 = 0,86 A

Bien, ya podemos calcular el voltaje que hay en cada una de las resistencias, puesto que tenemos el valor resistivo en ohmios y la intensidad en amperios.

Cuando solo sepamos el valor resistivo y la caída de tensión en una resistencia, aplicando la variante I = V/R hallaremos su intensidad. En resumidas cuentas, siempre vamos a tener 2 de los valores, y con la fórmula hallaremos el tercero.

Recordemos que:

Ra = R2 + R3 + R4

Rb = Ra en paralelo con R5

RT = R1 + Rb + R6

Ahora ya podemos calcular:

VR1 = IR1 * R1 = 0,86 * 3 =  2,58	IT = IR5 + IRa = 0,67 + 0,19 = 0,86 A
VRb = IR2 * Rb = 0,86 * 3,91 = 3,36	VR4 = IR4 * R4 = 0,19 * 8 = 1,52 V
VR6 = IR6 * R6 = 0,86 * 7 = 6,02	VR3 = IR3 * R3 = 0,19 * 6 = 1,14 V
IR5 = VRb/R5 = 3,36/5 = 0,67 A	VR2 = IR2 * R2 = 0,19 * 4 = 0,76 V
IRa = VRa/Ra = 3,36/18 = 0,19 A	VRb = VR4 + VR3 + VR2 = 3,42 V

VRa = V5 = VRb (Voltaje en Resistencias conectadas en paralelo)
IR1 = IRb = IR6 (Intensidad en Resistencias conectadas en serie)
IR2 = IR3 = IR4 = IRa (Intensidad en Resistencias conectadas en serie)

EQUIVALENTE DE LAS RESISTENCIAS EN PARALELO

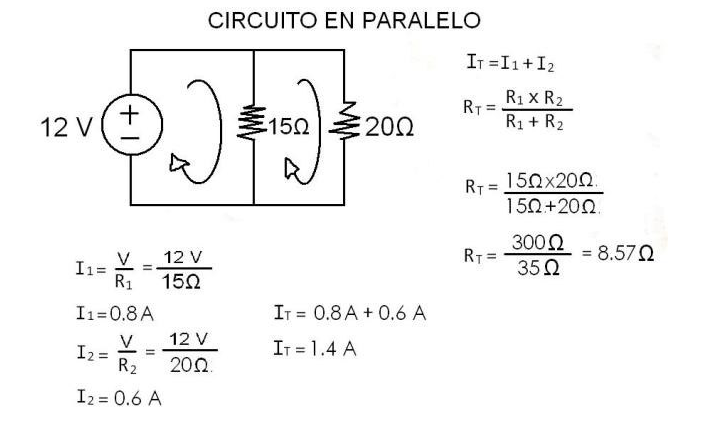
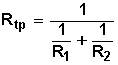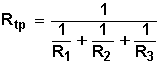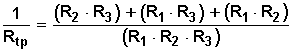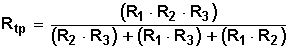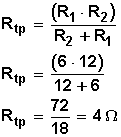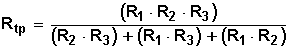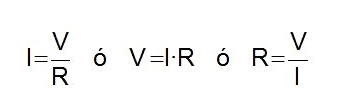EQUIVALENTE RESISTENCIAS EN PARALELO

Antes de entrar en materia es conveniente establecer el significado del concepto Resistencia equivalente.
Cuando en un circuito hay varias resistencias conectadas, resulta útil para calcular las corrientes que pasan por el circuito y las caídas de tensión que se producen, encontrar una resistencia que pueda sustituir a otras, de forma que el comportamiento del resto del circuito sea el mismo; o sea, debemos encontrar o calcular la Resistencia equivalente .
Esta resistencia equivalente, se sabe que existe, y para configuraciones en que las resistencias a sustituir están en paralelo o en serie, son fáciles de calcular como veremos más adelante.

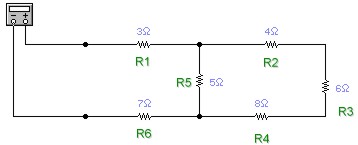
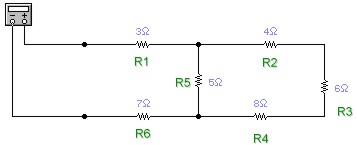
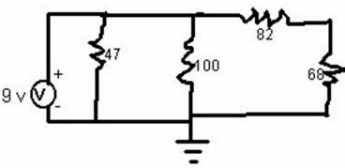
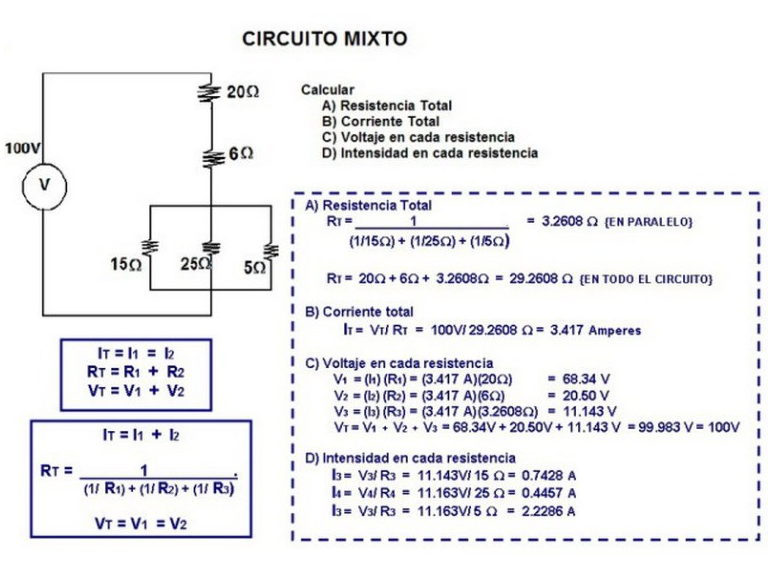
En ocasiones encontrarás resistencias en circuitos que no se pueden considerar exclusivamente en paralelo ni en serie, como en el diagrama de abajo (diagrama 1).

 

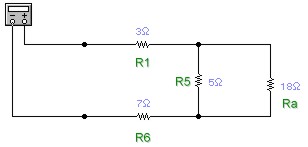
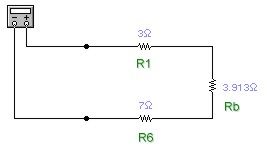
Las reglas para encontrar resistencias equivalentes a otras, ya sea en paralelo o en serie, se pueden aplicar de forma reiterada. Por ejemplo, si la resistencia equivalente a dos resistencias conectadas en serie (en el diagrama 82 ohm y 68 ohm) se encuentra en paralelo con otras, nada impide encontrar una resistencia equivalente a las dos en serie y después repetir el proceso con las que se encuentran en paralelo.

En general, para poder resolver este tipo de problemas se deben conocer las leyes básicas que cumplen la Intensidad (en amperios) y el voltaje (en voltios) cuando circulan a través de resistencias conectadas en serie o en paralelo, y la ley de Ohm :

Para resistencias en serie:
Pasando a través de resistencias en serie los voltios se reparten entre ellas (la tensión o voltaje).
Por todas las resistencias pasa la misma Intensidad de corriente (los amperios son los mismos en todas ellas; o sea, toda la corriente pasa por cada una de ellas).

Para resistencias en paralelo:
Pasando a través de las resistencias en paralelo los voltios son los mismos ya que sus extremos están en el mismo punto eléctrico (la tensión es la misma).
Pasando por las resistencias en paralelo los amperios se reparten entre ellas (sólo una parte del total de la intensidad de corriente pasa por cada una).

Ley de Ohm
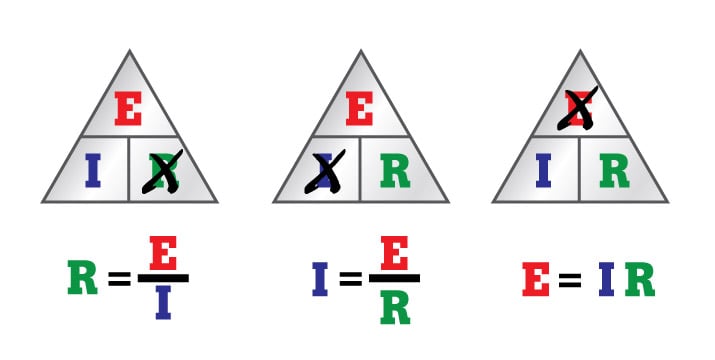
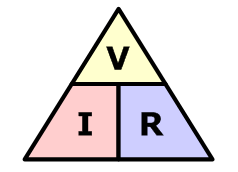
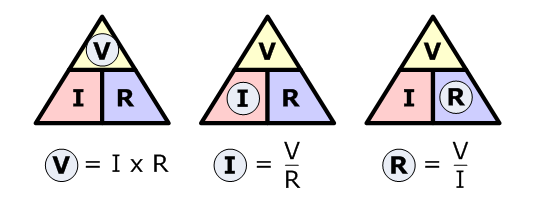
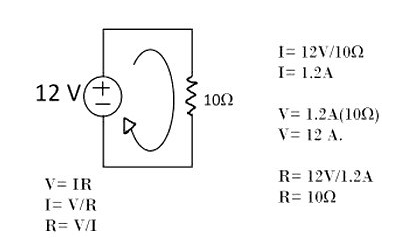
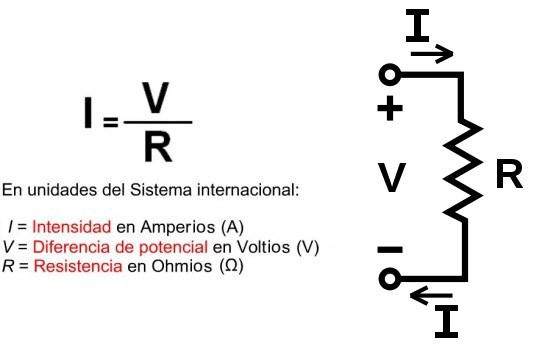
Según la ley de Ohm, cuando por una resistencia eléctrica "R", circula una corriente "I", se produce en ella una caída de tensión "V" entre los extremos de la resistencia cuyo valor viene dado por:

V = I * R

I = V/R

R = V/I

En el Sistema Internacional I (intensidad o corriente) viene dada en Amperios, V (voltaje o tensión) en Voltios y R (resistencia) en Ohmios.

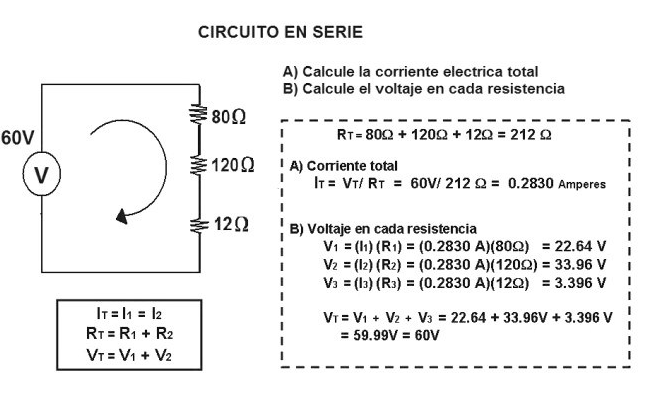
Resistencias (o resistores) en serie

Las resistencias en serie son aquellas que están conectadas una después de la otra.

El valor de la resistencia equivalente a las resistencias conectadas en serie es igual a la suma de los valores de cada una de ellas.

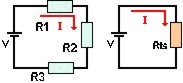
Diagrama 2

En este caso la corriente que fluye por las resistencias es la misma en todas.
Entonces:

R _ts (resistencia total serie) = R1 + R2 + R3

El valor de la corriente (Intensidad, en Amperios) en el circuito equivalente  (ver el diagrama 2) es el mismo que en el circuito original y se calcula con la ley de Ohm .

Una vez que se tiene el valor de la corriente que circula por el circuito, se pueden obtener las caídas de voltaje a través de cada una de las resistencias utilizando la ley de Ohm .

- En R1 la caída de voltaje es V1 = I x R1

- En R2 la caída de voltaje es V2 = I x R2

- En R3 la caída de voltaje es V3 = I x R3

Resistencias (resistores) en paralelo

Veíamos que en el circuito de resistencias en serie la corriente (Intensidad, en Amperios) circula sólo por un camino.
En el circuito de resistencias en paralelo la corriente (Intensidad, en Amperios) se divide y circula por varios caminos.
La resistencia total equivalente de un circuito de resistencias en paralelo (Rtp) es igual al recíproco de la suma de los inversos de las resistencias individuales.
Si tenemos un circuito con solo dos resistencias en paralelo, la fórmula sería:


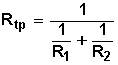
A su vez, el recíproco (o inverso multiplicativo) de esta fórmula será:


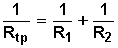
Al resolver (el m.c.m. es R1 • R2) , queda:


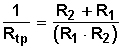
Y de nuevo recíprocamente:


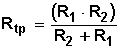
Veamos un ejemplo:
Calcular la resistencia total equivalente en un circuito formado por resistencias de 4 ohms y 6 ohms ubicadas en paralelo.
En la fómula anterior, reemplazamos los valores y queda:


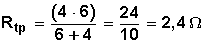
Veamos ahora qué sucede con la fórmula para un caso de tres resistencias en paralelo.
Recordemos:
La resistencia total equivalente de un circuito de resistencias en paralelo (Rtp) es igual al recíproco de la suma de los inversos de las resistencias individuales.
Si tenemos un circuito con tres resistencias en paralelo, la fórmula será:

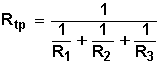
Presentando esta fórmula de manera ligeramente diferente (su forma recíproca), tendremos:


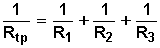
Desarrollando la ecuación, vemos que el mínimo común múltiplo (m.c.m.) del numerador de la suma de fracciones del término de la derecha es (R1 • R2 • R3) y hacemos

 
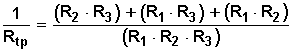
Como la ecuación indica el recíproco de Rtp, hacemos

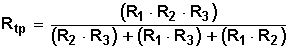
Un ejemplo:
Encontrar la resistencia equivalente de las siguientes resistencias.

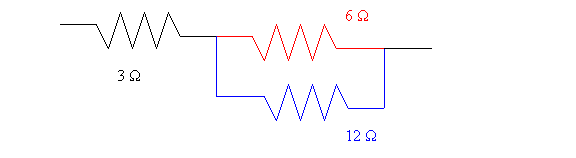
Tenemos una resistencia de 3 Ω en serie con un paralelo de dos resistencias.
Primero calculamos la resistencia en paralelo (resistencias roja y azul):
Aplicamos la fórmula


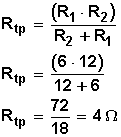
Luego se suman 3 + 4 = 7 Ω. Por tanto, la resistencia total equivalente es de 7 Ω.

Ejemplo:
Calcular la resistencia equivalente en un circuito formado por resistencias de 4 ohms, 6 ohms y 12 ohms ubicadas en paralelo.
Solución:
Aplicamos la fórmula



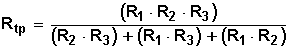
reemplazamos  y obtenemos


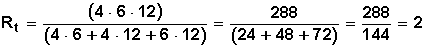
La resistencia total equivalente es igual a 2 ohms

Ley de Watt

Ley de watt

 

Fig. 3 Ley De Watt

Esta ley nos dice que "La potencia eléctrica es directamente proporcional al voltaje aplicado al dispositivo y la corriente que circula por el mismo"  con esta ecuación podemos hacer lo mismo que con la ley de ohm y podemos despejar las otras a través del triangulo en el centro de la Fig. 3 para poder llegar a la ecuaciones en lado derecho de la Fig. 3.

Hay algo interesante en las leyes de ohm y watt y es que se pueden unir para generar mas ecuaciones, al tener incógnitas en común se puede utilizar igualación o sustitución y quedarían como se muestra en la Fig. 4.

 

 

Fig. 3 Leyes De Ohm y Watt

Al combinar estas ecuaciones podemos calcular la potencia, la corriente, el voltaje y la resistencia al desconocer ciertos datos.

 

Potencia: Es la cantidad de energía entregada o absorbida por un elemento en un momento determinado

En el siguiente vídeo veremos una explicación mas sencilla y detallada sobre la ley de watt con algunos ejemplos.

 

Información tomada de : https://sites.google.com/site/tareainfobasica/condensadores/ley-de-watt 

La Ley de Ohm

¿Qué es la ley de Ohm?

La ley de Ohm se usa para determinar la relación entre tensión, corriente y resistencia en un circuito eléctrico.
Para los estudiantes de electrónica, la ley de Ohm (E = IR) es tan fundamental como lo es la ecuación de la relatividad de Einstein (E = mc²) para los físicos.
E = I x R
Cuando se enuncia en forma explícita, significa que tensión = corriente x resistencia, o voltios = amperios x ohmios, o V = A x Ω.
La ley de Ohm recibió su nombre en honor al físico alemán Georg Ohm (1789-1854) y aborda las cantidades clave en funcionamiento en los circuitos:

Cantidad	Símbolo de ley de Ohm	Unidad de medida (abreviatura)	Rol en los circuitos	En caso de que se esté preguntando:
Tensión	E	Voltio (V)	Presión que desencadena el flujo del electrones	E = fuerza electromotriz (término de la antigua escuela)
Corriente	I	Amperio (A)	Caudal de electrones	I = intensidad
Resistencia	R	Ohmio (Ω)	Inhibidor de flujo	Ω = Letra griega omega

Si se conocen dos de estos valores, los técnicos pueden reconfigurar la ley de Ohm para calcular el tercero. Simplemente, se debe modificar la pirámide de la siguiente manera:

Si conoce el voltaje (E) y la corriente (I) y quiere conocer la resistencia (R), suprima la R en la pirámide y calcule la ecuación restante (véase la pirámide primera o izquierda de arriba). Nota: la resistencia no puede medirse en un circuito en funcionamiento. Por lo tanto, para calcularla, la ley de Ohm es muy útil. En lugar de desconectar el circuito para medir la resistencia, un técnico puede determinar la R mediante la variación por sobre la ley de Ohm. Ahora, si usted conoce el voltaje (E) y la resistencia (R) y quiere conocer la corriente (I), suprima la I y calcule con los dos símbolos restantes (véase la pirámide media anterior). Y si conoce la corriente (I) y la resistencia (R) y quiere saber el voltaje (E), multiplique las mitades de la parte inferior de la pirámide (véase la tercera pirámide o la ubicada en el extremo derecho arriba). Pruebe con algunos cálculos de ejemplo basados en un circuito simple de la serie, que incluye una fuente de voltaje (batería) y resistencia (luz). Se conocen dos valores en cada ejemplo. Use la ley de Ohm para calcular el tercero. Información tomada de : https://www.fluke.com/es-co/informacion/mejores-practicas/aspectos-basicos-de-las-mediciones/electricidad/que-es-la-ley-de-ohm ¿Como se aplica La Ley de Ohm? La ley de Ohm se aplica a la totalidad de un circuito o a una parte del mismo. Analicemos la parte del circuito que analicemos, siempre se cumplirá. Solo a título informativo, comentar que para el análisis de circuitos de corriente alterna se sustituye la Resistencia (R) por la Impedancia (Z), que tiene en cuenta los desfases entre Voltaje e Intensidad y los efectos de los campos electromagnéticos producidos en los componentes electrónicos del circuito. Pero lo más normal en electrónica básica es analizar los circuitos en corriente continua o aplicar simplificaciones que nos permitan analizarlos como si lo fueran. De la ecuación anterior podemos despejar los valores de Voltaje y de Resistencia. De esta manera, conocidos o medidos dos de ellos, podremos calcular el tercero.   Aunque la fórmula no es difícil de recordar, existe una regla nemotécnica conocida como el Triángulo de la Ley de Ohm que facilita su uso.     En este triángulo, solo hay que tapar la variable que queremos calcular y aparecerán las otras dos variables con la posición que ocupan en la ecuación que corresponda.   Veamos como aplicar la ley en un circuito sencillo:   Si sabemos que el voltaje de la alimentación eléctrica es de 12 voltios y la resistencia del circuito es de 10 ohmios (el ohmio es la unidad de resistencia eléctrica y se representa por la letra griega Ω), aplicando la Ley de Ohm:                                               I = V / R = 12v / 10Ω = 1,2 Amperios En un circuito con varias resistencias en serie. Si sabemos el voltaje de alimentación, primero calcularemos la resistencia equivalente total sumando todas las resistencias que se encuentran en serie. Con este valor, aplicamos la Ley de Ohm como en el ejemplo anterior, y conocida la corriente que circula por el circuito, podemos calcular el voltaje en cada una de las resistencias, cuya suma, si no nos hemos equivocado, será el voltaje de alimentación:

En un circuito con resistencias en paralelo, conocemos el voltaje en los extremos de cada resistencia, por lo que podremos calcular de manera sencilla la corriente que circula por cada una de ellas. Y si calculamos la resistencia equivalente total aplicando las formulas de calculo para resistencias en paralelo, podremos comprobar que la corriente que circula por esta resistencia equivalente total es igual a la suma de las corrientes anteriormente calculadas que circula por cada una de las resistencias. En un circuito mixto de resistencias conectadas en serie y en paralelo, aplicaremos lo ya aprendido, pero dividiendo el circuito en subcircuitos de resistencias en función de cómo estén conectadas.   MUY IMPORTANTE tener en cuenta otro factor que completa la definición del circuito y los valores de sus resistencias. Estoy hablando de la Potencia eléctrica consumida en el circuito, que en el caso de las resistencias se transforma íntegramente en calor. “La potencia disipada en un circuito eléctrico es directamente proporcional al voltaje y la corriente que circula.” Por lo tanto:                                               W (watios) = V (voltios) x I (amperios) Así, por ejemplo, en el circuito más sencillo del primer ejemplo, la potencia de la resistencia deberá ser de al menos:                                                   W = V x I = 12v x 1,2A = 120 W Como seguramente no dispongamos de ninguna resistencia de esa potencia, y además sería muy voluminosa, lo mejor será utilizar para las pruebas resistencias de más de 1000Ω = 1 KiloOhmio = 1KΩ, de manera que en el ejemplo anterior:                                        W = V x I = V x  V / R  = V2 / R = 122 / 1000 = 0,144 W Podríamos utilizar una resistencia de 1KΩ y al menos 1/4 W (0,250 W). Y este mismo cálculo sería necesario realizarlo para cada una de las resistencias empleadas. Por cierto, que la unidad de resistencia eléctrica sea el Ohmio no es casualidad, recibe este nombre como homenaje a George Simon Ohm. La Ley de Ohm establece que "La intensidad de la corriente eléctrica que circula por un conductor es directamente proporcional a la diferencia de potencial aplicada e inversamente proporcional a la resistencia del mismo", se puede expresar matemáticamente donde, empleando unidades del Sistema internacional, tenemos que:  • I = Intensidad en amperios (A)  • V = Diferencia de potencial en voltios (V) • R = Resistencia en ohmios (Ω). Esta ley no se cumple, por ejemplo, cuando la resistencia del conductor varía con la temperatura, y la temperatura del conductor depende de la intensidad de corriente y el tiempo que esté circulando. La ley define una propiedad específica de ciertos materiales por la que se cumple la relación: Un conductor cumple la Ley de Ohm sólo si su curva V-I es lineal, esto es si R es independiente de V y de I. En general: v=i.R Ley Ohm LEY DE OHM: George Simon Ohm, formuló en 1827 la que se conoce como Ley de Ohm. Posiblemente una de las leyes fundamentales de la electrónica. Primero definió matemáticamente las tres magnitudes físicas principales de la electrónica: Diferencia de Potencial (o Voltaje), Resistencia y Corriente (o Intensidad) La Ley de Ohm relaciona estas tres magnitudes físicas, siendo su enunciado el siguiente: La Corriente que circula por un circuito eléctrico varía de manera directamente proporcional a la Diferencia de Potencial, e inversamente proporcional con la Resistencia del circuito. Su formulación matemática es: La ley de Ohm se aplica a la totalidad de un circuito o a una parte del mismo. Analicemos la parte del circuito que analicemos, siempre se cumplirá. Solo a título informativo, comentar que para el análisis de circuitos de corriente alterna se sustituye la Resistencia (R) por la Impedancia (Z), que tiene en cuenta los desfases entre Voltaje e Intensidad y los efectos de los campos electromagnéticos producidos en los componentes electrónicos del circuito. Pero lo más normal en electrónica básica es analizar los circuitos en corriente continua o aplicar simplificaciones que nos permitan analizarlos como si lo fueran. De la ecuación anterior podemos despejar los valores de Voltaje y de Resistencia. De esta manera, conocidos o medidos dos de ellos, podremos calcular el tercero. Aunque la fórmula no es difícil de recordar, existe una regla nemotécnica conocida como el Triángulo de la Ley de Ohm que facilita su uso.                                                                               Triángulo de la Ley de Ohm En este triángulo, solo hay que tapar la variable que queremos calcular y aparecerán las otras dos variables con la posición que ocupan en la ecuación que corresponda. Veamos como aplicar la ley en un circuito sencillo: Si sabemos que el voltaje de la alimentación eléctrica es de 12 voltios y la resistencia del circuito es de 10 ohmios (el ohmio es la unidad de resistencia eléctrica y se representa por la letra griega Ω), aplicando la Ley de Ohm:                                               I = V / R = 12v / 10Ω = 1,2 Amperios En un circuito con varias resistencias en serie. Si sabemos el voltaje de alimentación, primero calcularemos la resistencia equivalente total sumando todas las resistencias que se encuentran en serie. Con este valor, aplicamos la Ley de Ohm como en el ejemplo anterior, y conocida la corriente que circula por el circuito, podemos calcular el voltaje en cada una de las resistencias, cuya suma, si no nos hemos equivocado, será el voltaje de alimentación: En un circuito con resistencias en paralelo, conocemos el voltaje en los extremos de cada resistencia, por lo que podremos calcular de manera sencilla la corriente que circula por cada una de ellas. Y si calculamos la resistencia equivalente total aplicando las formulas de calculo para resistencias en paralelo, podremos comprobar que la corriente que circula por esta resistencia equivalente total es igual a la suma de las corrientes anteriormente calculadas que circula por cada una de las resistencias. En un circuito mixto de resistencias conectadas en serie y en paralelo, aplicaremos lo ya aprendido, pero dividiendo el circuito en subcircuitos de resistencias en función de cómo estén conectadas.

Código de colores de las resistencias

El código de colores de resistencia funciona a base de colores. En la actualidad existen una gran variedad de resistencias, son  indispensables para los circuitos que utilizamos hoy en día. Analizaremos el código de colores de  las resistencias para averiguar los valores que tienen. Este código es de gran utilidad debido a que no siempre tendremos un aparato como un multimetro. Recordemos que la unidad de medida de estos componentes es el Ohm.
El código de colores de resistencia nos indica cuantos Ohms tiene esa resistencia. Además nos indica otros parámetros que veremos a continuación.Hay resistencias que sus valores vienen impresos sobre ellas, ya que tienen un tamaño grande. Pero cuando son muy pequeñas es más difícil, de manera que es mejor utilizar un código de colores en las resistencias para que allá una mejor facilidad de manejar el componente.

 Resistencias de 4 y 5 bandas

Estas resistencias cada color representa un valor, como en el caso de la primera (1) le agregaremos su valor con la tabla inferior.

Las primeras dos bandas establecen el valor del resistor como en el caso del primer color es  (verde). Podemos observar, que en la tabla el color equivale a 5 entonces es  la primer cifra.  Luego la segunda banda es de color  (blanco) observamos de nuevo en la tabla su valor es 9 esta seria la segunda cifra. La tercera es el multiplicador en esta es la que nos  indicara los ceros  al final,  la tercera es de color  café esta vale un 0 y posteriormente encontraremos su  valor que es 590 Ohm

 

Tabla del código de colores de las resistencias

 

 La cuarta banda de color dorado que es la tolerancia, es donde la resistencia tiene un porcentaje. En el cual el valor de la resistencia se puede encontrar entre  un valor máximo y un mínimo. Como la resistencia es de 590 Ohm pero tiene una tolerancia de 5%. Entonces su valor máximo sería 619.5 Ohm y el valor mínimo 560.5 Ohm.

La resistencia tendría cualquier  valor que  estaría entre el rango del valor máximo y mínimo (619.5 – 560.5).
Entonces no sería precisamente los 590 Ohm, a causa de la tolerancia. También en  código de colores de resistencia, en la banda de la tolerancia para no utilizar tantos ceros simplificamos con múltiplos una K (Kilo) o M(Mega). Por ejemplo hay veces que  es necesario hacer alguna operación y  podríamos confundirnos con demasiados ceros. La K equivalen 3 ceros y la M 6 , existen mas múltiplos pero estos son los comunes.
Un ejemplo con una resistencia de 1000 Ohm  esta seria 1k 0hm. Otro ejemplo de 4700 esta aplica igual se pone 4 luego un punto esto para indicar que ya no son miles 4.7K entonces para una de 1000,000 esta es 1M 0hm.
También están las resistencias de 5 bandas. Para estas aplica lo mismo lo que cambia es la multiplicadora sería la cuarta banda. Entonces las tres primeras bandas son los valores a indicar cuál es la necesaria y la quinta es la tolerancia.

 

 

Si la resistencia tiene la tolerancia mínima se obtendrá más cercano al valor deseado.

¿Cuál es la causa de que existan estas tolerancias?

Porque hay valores de resistencias en los circuitos,  que  no son muy comunes, entonces es muy difícil encontrarlas en el mercado. Con la tolerancia te pueden ser útil para llegar aproximado  al valor deseado a la hora de realizar un proyecto.
Los valores comerciales mas comunes son de 100, 220, 330, 1K, 4.7k y 10k.

 Información tomada de : https://hetpro-store.com/TUTORIALES/codigo-de-colores-de-resistencia/