La Ley de Ohm

¿Qué es la ley de Ohm?

La ley de Ohm se usa para determinar la relación entre tensión, corriente y resistencia en un circuito eléctrico.
Para los estudiantes de electrónica, la ley de Ohm (E = IR) es tan fundamental como lo es la ecuación de la relatividad de Einstein (E = mc²) para los físicos.
E = I x R
Cuando se enuncia en forma explícita, significa que tensión = corriente x resistencia, o voltios = amperios x ohmios, o V = A x Ω.
La ley de Ohm recibió su nombre en honor al físico alemán Georg Ohm (1789-1854) y aborda las cantidades clave en funcionamiento en los circuitos:

Cantidad	Símbolo de ley de Ohm	Unidad de medida (abreviatura)	Rol en los circuitos	En caso de que se esté preguntando:
Tensión	E	Voltio (V)	Presión que desencadena el flujo del electrones	E = fuerza electromotriz (término de la antigua escuela)
Corriente	I	Amperio (A)	Caudal de electrones	I = intensidad
Resistencia	R	Ohmio (Ω)	Inhibidor de flujo	Ω = Letra griega omega

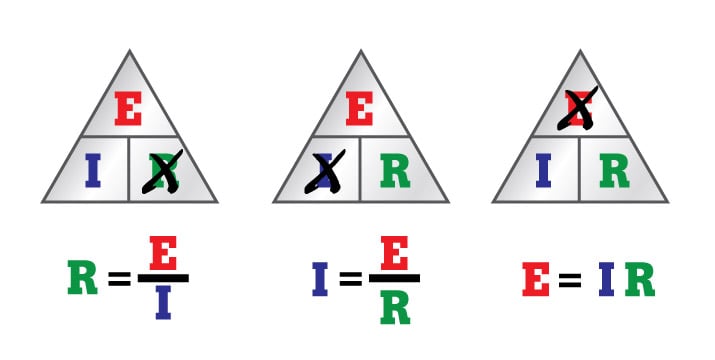
Si se conocen dos de estos valores, los técnicos pueden reconfigurar la ley de Ohm para calcular el tercero. Simplemente, se debe modificar la pirámide de la siguiente manera:

Si conoce el voltaje (E) y la corriente (I) y quiere conocer la resistencia (R), suprima la R en la pirámide y calcule la ecuación restante (véase la pirámide primera o izquierda de arriba). Nota: la resistencia no puede medirse en un circuito en funcionamiento. Por lo tanto, para calcularla, la ley de Ohm es muy útil. En lugar de desconectar el circuito para medir la resistencia, un técnico puede determinar la R mediante la variación por sobre la ley de Ohm. Ahora, si usted conoce el voltaje (E) y la resistencia (R) y quiere conocer la corriente (I), suprima la I y calcule con los dos símbolos restantes (véase la pirámide media anterior). Y si conoce la corriente (I) y la resistencia (R) y quiere saber el voltaje (E), multiplique las mitades de la parte inferior de la pirámide (véase la tercera pirámide o la ubicada en el extremo derecho arriba). Pruebe con algunos cálculos de ejemplo basados en un circuito simple de la serie, que incluye una fuente de voltaje (batería) y resistencia (luz). Se conocen dos valores en cada ejemplo. Use la ley de Ohm para calcular el tercero. Información tomada de : https://www.fluke.com/es-co/informacion/mejores-practicas/aspectos-basicos-de-las-mediciones/electricidad/que-es-la-ley-de-ohm ¿Como se aplica La Ley de Ohm? La ley de Ohm se aplica a la totalidad de un circuito o a una parte del mismo. Analicemos la parte del circuito que analicemos, siempre se cumplirá. Solo a título informativo, comentar que para el análisis de circuitos de corriente alterna se sustituye la Resistencia (R) por la Impedancia (Z), que tiene en cuenta los desfases entre Voltaje e Intensidad y los efectos de los campos electromagnéticos producidos en los componentes electrónicos del circuito. Pero lo más normal en electrónica básica es analizar los circuitos en corriente continua o aplicar simplificaciones que nos permitan analizarlos como si lo fueran. De la ecuación anterior podemos despejar los valores de Voltaje y de Resistencia. De esta manera, conocidos o medidos dos de ellos, podremos calcular el tercero.   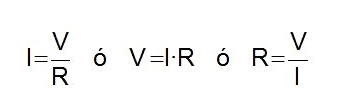Aunque la fórmula no es difícil de recordar, existe una regla nemotécnica conocida como el Triángulo de la Ley de Ohm que facilita su uso. 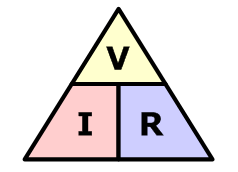    En este triángulo, solo hay que tapar la variable que queremos calcular y aparecerán las otras dos variables con la posición que ocupan en la ecuación que corresponda. 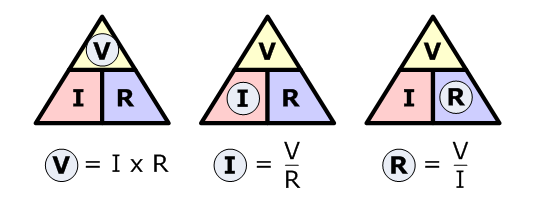  Veamos como aplicar la ley en un circuito sencillo: 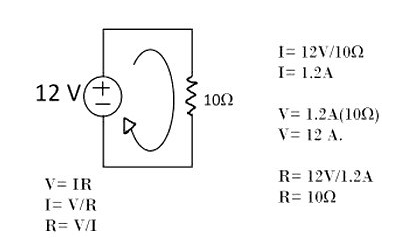  Si sabemos que el voltaje de la alimentación eléctrica es de 12 voltios y la resistencia del circuito es de 10 ohmios (el ohmio es la unidad de resistencia eléctrica y se representa por la letra griega Ω), aplicando la Ley de Ohm:                                               I = V / R = 12v / 10Ω = 1,2 Amperios En un circuito con varias resistencias en serie. Si sabemos el voltaje de alimentación, primero calcularemos la resistencia equivalente total sumando todas las resistencias que se encuentran en serie. Con este valor, aplicamos la Ley de Ohm como en el ejemplo anterior, y conocida la corriente que circula por el circuito, podemos calcular el voltaje en cada una de las resistencias, cuya suma, si no nos hemos equivocado, será el voltaje de alimentación:

En un circuito con resistencias en paralelo, conocemos el voltaje en los extremos de cada resistencia, por lo que podremos calcular de manera sencilla la corriente que circula por cada una de ellas. Y si calculamos la resistencia equivalente total aplicando las formulas de calculo para resistencias en paralelo, podremos comprobar que la corriente que circula por esta resistencia equivalente total es igual a la suma de las corrientes anteriormente calculadas que circula por cada una de las resistencias. En un circuito mixto de resistencias conectadas en serie y en paralelo, aplicaremos lo ya aprendido, pero dividiendo el circuito en subcircuitos de resistencias en función de cómo estén conectadas.   MUY IMPORTANTE tener en cuenta otro factor que completa la definición del circuito y los valores de sus resistencias. Estoy hablando de la Potencia eléctrica consumida en el circuito, que en el caso de las resistencias se transforma íntegramente en calor. “La potencia disipada en un circuito eléctrico es directamente proporcional al voltaje y la corriente que circula.” Por lo tanto:                                               W (watios) = V (voltios) x I (amperios) Así, por ejemplo, en el circuito más sencillo del primer ejemplo, la potencia de la resistencia deberá ser de al menos:                                                   W = V x I = 12v x 1,2A = 120 W Como seguramente no dispongamos de ninguna resistencia de esa potencia, y además sería muy voluminosa, lo mejor será utilizar para las pruebas resistencias de más de 1000Ω = 1 KiloOhmio = 1KΩ, de manera que en el ejemplo anterior:                                        W = V x I = V x  V / R  = V2 / R = 122 / 1000 = 0,144 W Podríamos utilizar una resistencia de 1KΩ y al menos 1/4 W (0,250 W). Y este mismo cálculo sería necesario realizarlo para cada una de las resistencias empleadas. Por cierto, que la unidad de resistencia eléctrica sea el Ohmio no es casualidad, recibe este nombre como homenaje a George Simon Ohm. La Ley de Ohm establece que "La intensidad de la corriente eléctrica que circula por un conductor es directamente proporcional a la diferencia de potencial aplicada e inversamente proporcional a la resistencia del mismo", se puede expresar matemáticamente donde, empleando unidades del Sistema internacional, tenemos que:  • I = Intensidad en amperios (A)  • V = Diferencia de potencial en voltios (V) • R = Resistencia en ohmios (Ω). Esta ley no se cumple, por ejemplo, cuando la resistencia del conductor varía con la temperatura, y la temperatura del conductor depende de la intensidad de corriente y el tiempo que esté circulando. La ley define una propiedad específica de ciertos materiales por la que se cumple la relación: Un conductor cumple la Ley de Ohm sólo si su curva V-I es lineal, esto es si R es independiente de V y de I. En general: v=i.R Ley Ohm LEY DE OHM: George Simon Ohm, formuló en 1827 la que se conoce como Ley de Ohm. Posiblemente una de las leyes fundamentales de la electrónica. Primero definió matemáticamente las tres magnitudes físicas principales de la electrónica: Diferencia de Potencial (o Voltaje), Resistencia y Corriente (o Intensidad) La Ley de Ohm relaciona estas tres magnitudes físicas, siendo su enunciado el siguiente: La Corriente que circula por un circuito eléctrico varía de manera directamente proporcional a la Diferencia de Potencial, e inversamente proporcional con la Resistencia del circuito. 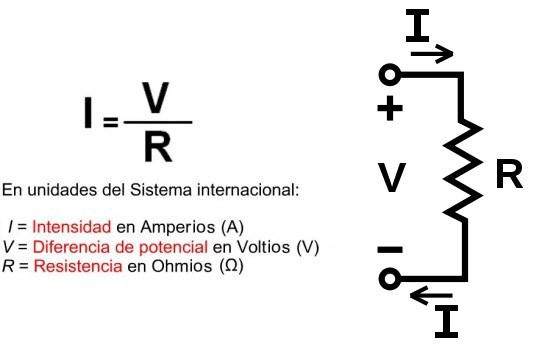Su formulación matemática es: La ley de Ohm se aplica a la totalidad de un circuito o a una parte del mismo. Analicemos la parte del circuito que analicemos, siempre se cumplirá. Solo a título informativo, comentar que para el análisis de circuitos de corriente alterna se sustituye la Resistencia (R) por la Impedancia (Z), que tiene en cuenta los desfases entre Voltaje e Intensidad y los efectos de los campos electromagnéticos producidos en los componentes electrónicos del circuito. Pero lo más normal en electrónica básica es analizar los circuitos en corriente continua o aplicar simplificaciones que nos permitan analizarlos como si lo fueran. De la ecuación anterior podemos despejar los valores de Voltaje y de Resistencia. De esta manera, conocidos o medidos dos de ellos, podremos calcular el tercero. 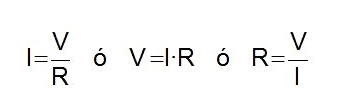Aunque la fórmula no es difícil de recordar, existe una regla nemotécnica conocida como el Triángulo de la Ley de Ohm que facilita su uso.                                                                               Triángulo de la Ley de Ohm En este triángulo, solo hay que tapar la variable que queremos calcular y aparecerán las otras dos variables con la posición que ocupan en la ecuación que corresponda. 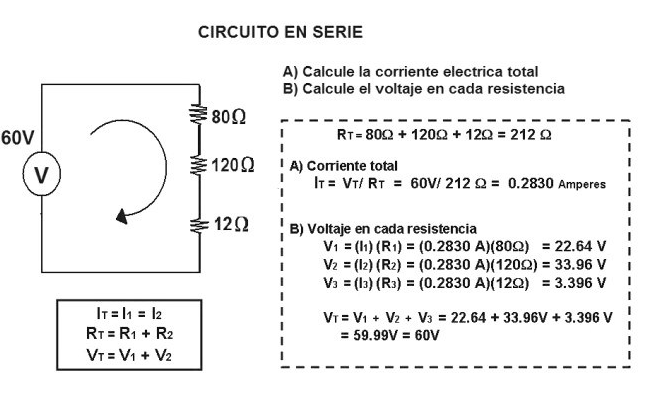Veamos como aplicar la ley en un circuito sencillo: Si sabemos que el voltaje de la alimentación eléctrica es de 12 voltios y la resistencia del circuito es de 10 ohmios (el ohmio es la unidad de resistencia eléctrica y se representa por la letra griega Ω), aplicando la Ley de Ohm:                                               I = V / R = 12v / 10Ω = 1,2 Amperios En un circuito con varias resistencias en serie. Si sabemos el voltaje de alimentación, primero calcularemos la resistencia equivalente total sumando todas las resistencias que se encuentran en serie. 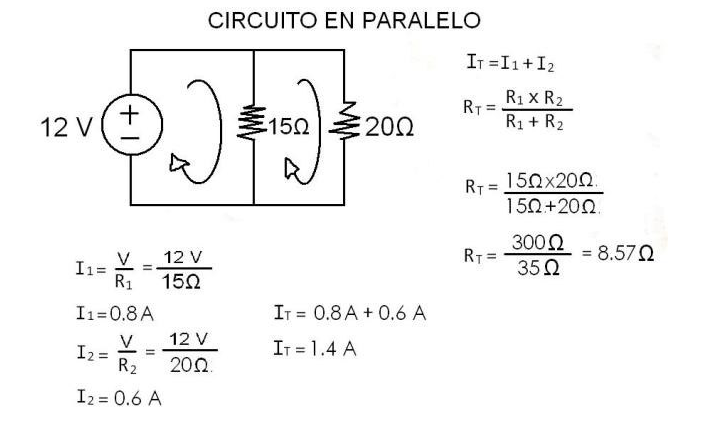Con este valor, aplicamos la Ley de Ohm como en el ejemplo anterior, y conocida la corriente que circula por el circuito, podemos calcular el voltaje en cada una de las resistencias, cuya suma, si no nos hemos equivocado, será el voltaje de alimentación: En un circuito con resistencias en paralelo, conocemos el voltaje en los extremos de cada resistencia, por lo que podremos calcular de manera sencilla la corriente que circula por cada una de ellas. Y si calculamos la resistencia equivalente total aplicando las formulas de calculo para resistencias en paralelo, podremos comprobar que la corriente que circula por esta resistencia equivalente total es igual a la suma de las corrientes anteriormente calculadas que circula por cada una de las resistencias. 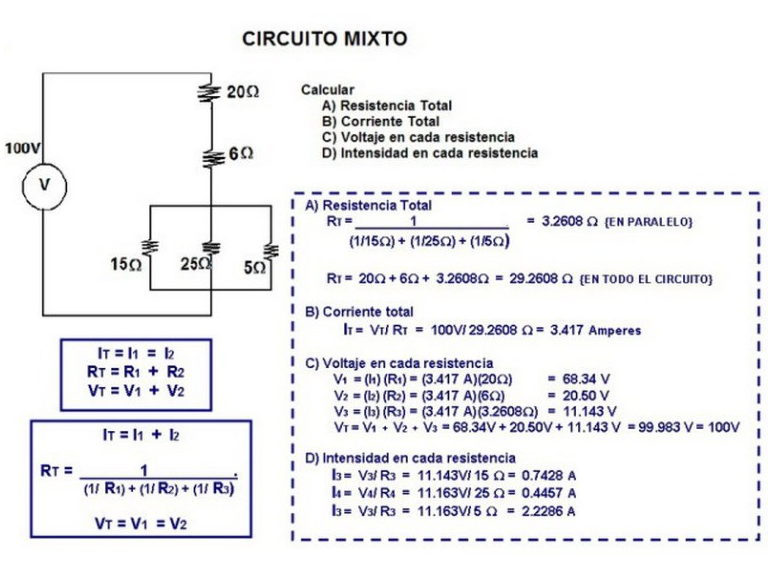En un circuito mixto de resistencias conectadas en serie y en paralelo, aplicaremos lo ya aprendido, pero dividiendo el circuito en subcircuitos de resistencias en función de cómo estén conectadas.